Willkommen in der Planckwelt

4. Interview in München

Die Symmetrie der Masse

IZ:
Wir treffen uns in München zu unserem 4. Interview und vertiefen die Themen des letzten Interviews weiter. Wir sprachen über das erweiterte Standardprogramm der Elementarteilchen, über das Massenspektrum der Elementarteilchen und seine Symmetrie, über die mögliche Erzeugung von ultraschweren Wasserstoff am LHC, über die Dunkle Materie, über die Entstehung von Aminosäuren auf Kometen und über die Attophysik , mit der Elektronen mit Laserphotonen mit einer Belichtungszeit von 10^-18 sec fotografiert werden und so in Raum und Zeit aufgelöst werden.
Inzwischen wurden auch die Gravitationswellen in einem aufwändigen Experiment nachgewiesen. Wozu benötigen wir eigentlich eine Symmetrie der Elementarteilchenmassen ?

Autor:
Obwohl mit dem Standardmodell der Elementarteilchen die experimentellen Ergebnisse an den Beschleunigern mit hoher Präzision abgebildet werden können, bereitet es doch allgemeines Unbehagen bei den Physikern. Das liegt an den zahlreichen freien Parametern, die nicht von den Naturkonstanten abgeleitet werden können. Die experimentell ermittelten Werte müssen in das Standardprogramm eingegeben werden, damit die Werte aus den Streuexperimenten berechnet werden können. Zu den freien Parametern gehören auch die 12 Massen der Quarks und Leptonen. Eine Symmetrie der Masse würde die Beliebigkeit der Massen beenden und die Anzahl der freien Parameter reduzieren. Weiterhin ist nach der herrschenden Lehre das Standardmodell der Elementarteilchen unvollständig, weil es die Gravitationskraft nicht enthält. Es beschreibt hingegen sehr gut die elektromagnetische Kraft, die schwache Kraft und die starke Kernkraft.

IZ:
Macht es wegen der Unschärferelation von Heisenberg überhaupt Sinn, sich im Mikrokosmos mit Bewegungen von massiven Teilchen in Raum und Zeit zu beschäftigen ? Wir verbinden Gravitation mit der Anziehung von Massen. Die gravitative Anziehung der Elementarteilchen ist aufgrund der kleinen Massen so gering, dass sie überhaupt nicht gemessen werden kann. Die Gravitationskraft wird im Mikrokosmos überlagert von der viel stärkeren elektroschwachen Kraft und der Kernkraft.

Autor:
Wir sollten im Mikrokosmos nicht von der Schwerkraft sprechen sondern von der Trägheitskraft. Einstein betrachtete es als den glücklichsten Einfall seines Lebens, als er erkannte, dass Schwerkraft und Trägheitskraft nur 2 Medaillen des gemeinsamen gravito-inertialen Feldes sind. Er formulierte seine Einsicht im Äquivalenzprinzip von schwerer und träger Masse. Im Mikrokosmos sollten wir uns nur mit der Trägheitskraft beschäftigen, die bewirkt, dass Teilchen aufgrund ihrer Ruhemasse sich mit einer Geschwindigkeit kleiner als der Lichtgeschwindigkeit bewegen. Photonen und Gluonen haben keine Ruhemasse. Sie bewegen sich mit Lichtgeschwindigkeit.

IZ:
Gibt es im Kosmos Abweichungen von den Gravitationsgesetzen, die mit dem Standardmodell der Elementarteilchen erklärt werden können ?

Autor:
Die Bewegungskurven leuchtender Sterne in fernen Galaxien weichen von den Bewegungsgesetzen der Gravitationstheorie von Newton ab. Das wird durch die Anwesenheit von Dunkler Materie erklärt. Gemessen wird dabei die Doppler-Verschiebung der 21cm-Linie des Wasserstoffs. Da sich die 3 Familien der Quarks und Leptonen nur durch ihre Massen unterscheiden, kann nicht ausgeschlossen werden, dass die größere Dichte der Wasserstoffwolken durch ultraschweren Wasserstoff erzeugt wird. Dieser ultraschwere Wasserstoff würde aus den Quarks und dem Lepton der 2. Familie bestehen.

IZ:
Sie meinen also, dass man das Gravitationsgesetz von Newton den experimentellen Ergebnissen der Astrophysik mit einer Wasserstoff-Form mit größeren Dichte anpassen kann. Ultraschwerer Wasserstoff ist viermal so schwer wie normaler Wasserstoff. Kommen wir wieder zurück zur Symmetrie der Elementarteilchenmassen. Entwickeln wir schrittweise die Symmetrie der Elementarteilchenmassen.

Autor:
Im Standardmodell haben die Bosonen, Quarks und Leptonen 15 verschiedene Massen. Sie werden nach dem Higgsmechanismus durch die unterschiedliche Kopplung an das skalare Higgsfeld erzeugt. Die 15 Yukawa- Kopplungskoeffizienten werden mit f=m/v berechnet. Durch die Bildung von Masseverhältnissen ist man die Dimension los , die bei der Berechnung der Ergebnisse von Streuexperimenten zu unsinnigen Ergebnissen führt. Diese Yukawa-Koeffizienten können als Masseladungen angesehen werden. Sie werden von der Eulerschen Zahl e abgeleitet und haben somit eine solide Basis.

IZ:
Berechnen wir die Massen der Bosonen, der Quarks und der geladenen Leptonen und vergleichen sie mit den an den Beschleunigern experimentell ermittelten Massen.

Autor:
Wir gehen aus vom Vakuumerwartungswert v = 246 GeV und seinem Zerfallsmodus. Historisch sind die Physiker den umgekehrten Weg gegangen . Mit immer größere Beschleunigungsenergien weisen sie die nächst größeren Massen der Elementarteilchen nach. Der Vakuumerwartungswert zerfällt nach folgenden Gleichungen, vergleichbar mit dem radioaktiven Zerfall :


v h Z –Bosonen: m=v e^- ( 1/3 n )
t µ e –Leptonen : m= v e^- ( e n - e^(-2/3))
b s d – Quarks : m= v e^-( e²/ 2 n +1/3 )
t c u - Quarks : m= v e^-( 2e²/3 n +1/3 )

Mit den Quantenzahlen n berechnen sich die Massen in [GeV] wie folgt:

n [GeV] n [GeV] n [GeV]
v h Z 0 246 2 126.3 3 90.5
t µ e 2 1.8 3 0.118 5 0.00051
b s d 1 4.4 2 0.109 3 0.0027
t c u 0 176 1 1.3 2 0.0093

Die experimentellen Werte sind:

v h Z 246 126.3 91
τ µ e 1.8 0.1 0.0005
b s d 4.7 0.15 0.007
t c u 174 1.5 0.004

IZ:
Sie haben in der Grafik das Massenspektrum des Standardmodells der Elementarteilchen unter Berücksichtigung der Massenwerte dargestellt. Das ist neu und es beeindruckt mich sehr ! Durch einen einfachen Algorithmus auf Basis der Zahl e tragen die Massen Quantenzahlen. Es geht um die grundlegende Frage: Lässt sich die Wirklichkeit analog oder digital abbilden, durch ein kontinuierliches Feld oder durch einen Algorithmus mit Quantenzahlen ? . Kommen wir jetzt nach diesen tiefsinnigen Gedanken zu den Symmetrieüberlegungen.

Autor:

In der Grafik 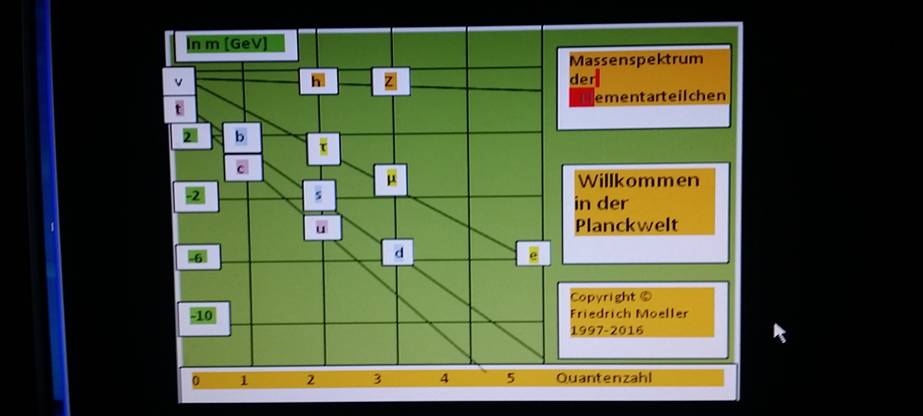lassen sich die 15 Massen durch Rotation und Translation ineinander überführen.
Die logarithmischen Massenwerte entsprechen Punkten auf Geraden mit 4 unterschiedlichen negativen Steigungswinkeln. Die x-Werte sind Quantenzahlen. Die Geraden treffen die logarithmische y-Achse nicht in einem Punkt. Sie sind verschoben. Die Bosonen- Gerade schneidet die Y-Achse beim Vakuumerwartungswert v=246 GeV. Die beiden Quark-Geraden sind um +1/3 verschoben, die Lepton-Gerade um – e^(-2/3) . Wir können das auch so interpretieren, dass Bosonen, Quarks und Leptonen unterschiedliche Vakuumerwartungswerte haben. Die Massen der Elementarteilchen werden durch eine Symmetrie ineinander überführt, die die Rotation und die xy-Translation einschließt.

IZ:
Können Sie das anhand einiger Beispiele erklären ?

Autor:
Die oberste Gerade der Bosonen hat die Steigung tanα = -1/3. Sie schneidet die Y-Achse beim Vakuumerwartungswert v=246 GeV. Das Higgs-Boson hat auf dieser Geraden die Quantenzahl x=2. Der y-Wert ist -2/3 . Der Wert v e^(-2/3) = 126.5 GeV ist der Wert , der am Atlas-Detektor gemessen wurde. Die Werte x=2 und y=-2/3 überraschen, weil nach der herrschenden Lehre die Masse des Higgs-Bosons ein freier Parameter ist und nicht berechnet werden kann und damit der immense experimentelle Aufwand am LHC notwendig wurde.

Autor:
Die Symmetrien des Standardmodells sind SU(3) x (SU(2) x U(1) . Die SU(2) ist eine unitäre Rotationssymmetrie im 2-dimensionalen Raum. Aus dieser Symmetrie ergeben sich 2²-1 =3 Vektorbosonen der schwachen Kraft. Die SU(3) ist eine unitäre Rotationssymmetrie im 3-dimensionalen Raum. Aus dieser Symmetrie ergeben sich die 3²-1 = 8 Gluonen als Eichbosonen der starken Kraft. Die Massen der Elementarteilchen werden erzeugt durch unterschiedliche Kopplung an das Higgs-Feld. Die 15 Massen haben 4²-1 = 15 unterschiedliche Yukawa-Kopplungskoeffizienten. Zur 3-dimensionalen Drehung kommt die Translation hinzu, und wir können eine Symmetrie in einem 4-dimensionalen Raum definieren.

IZ:
Wie sieht die Symmetrie aus ?

Autor:
Im Standardmodell der Elementarteilchen sind die Massen beliebig. Erst eine Symmetrie beendet die Beliebigkeit. In der logarithmischen Darstellung der Massen haben Massen gleiche Abstände. Massen unterliegen der Skalensymmetrie. Beim Zerfall muss die Ladungserhaltung der elektromagnetischen Kraft, der schwachen Kraft, und der starken Kraft beachtet werden. Die Symmetrien SU(4) x SU(3) x SU(2) x U(1) müssen über die Ladungserhaltung zusammenpassen. Die SU(4) wird mit der Rotation um den Vakuumerwartungswert v und der Translation in x- und y-Richtung durch eine homogene 4x4-Matrix dargestellt. Durch die Rotation verändern sich die Abstände in der Skalensymmetrie. Werden die Drehungen auf die Ebene projiziert, erhalten wir die Drehwinkel wie folgt.

tan α Drehwinkel Spin Ladung
Bosonen -0.33 = -1/3 -18.5 ° 1 0
Leptonen -2.71 = -e -69.8 ° ½ 1
d-Quarks -3.71 = -e²/2 -74.9 ° ½ -1/3
u-Quarks -4.96 = -2e²/3 -78.6 ° ½ +2/3
Neutrinos - 7.39 = -e² -82.3 ° 1/2 0

IZ:
Die Massen der Elementarteilchen sind skalensymmetrisch. Die starke Kraft, die schwache Kraft und die elektromagnetische Kraft sind eichsymmetrisch. Wir haben uns mit einer möglichen vierdimensionalen Symmetrie des Massenspektrums der Elementarteilchen beschäftigt. In unserem nächsten Interview in München beschäftigen wir uns mit der Feinstrukturkonstante α, die Sommerfeld 1916 eingeführt hat. Sie ist die Kopplungskonstante der elektromagnetischen Wechselwirkung. Die dimensionslose Zahl 1/137 ist ein Mysterium und viele berühmte Physiker haben über diese Zahl gegrübelt . Können wir das Rätsel mit unserem 5. Interview in München lösen ?

Copyright © Friedrich Moeller 1997-2016 Email: f.moeller@necnet.de