i Willkommen in der Planckwelt

Gibt es die Quantengravitation ?
5. Interview in Hannover

IZ:
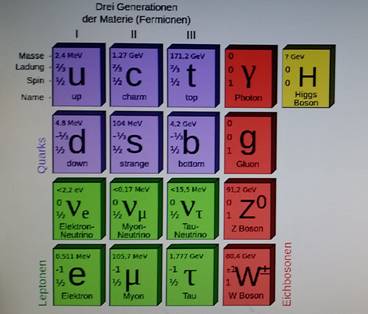
Die Familienzahlen sind Quantenzahlen der Masse. Das ist eine großartige Erkenntnis. Peter Higgs verdanken wir eine neues Verständnis der Masse. Er postulierte das Higgs-Boson als Anregung des skalaren Higgsfeldes . Die Frage , warum sein Higgs-Boson die Masse hat, die es hat, kann bis heute nicht beantwortet werden. Als Albert Einstein vor 100 Jahren die Gravitationswellen vorausgesagte, konnte er sich ihren Nachweis damals nicht vorstellen. Erst mit hochentwickelter Lasertechnik aus Hannover wurden die Gravitationswellen mit den beiden LIGO-Detektoren in den USA nachgewiesen. Der Nachweis wurde 2017 mit dem Nobelpreis belohnt. Vor 100 Jahren hat Einstein mit seiner Allgemeinen Relativitätstheorie die Gravitation als Krümmung der Raumzeit erklärt. Unabhängig davon wurde die Quantentheorie entwickelt. Die Allgemeine Relativitätstheorie beschreibt die Welt erfolgreich im Großen, die Quantentheorie die Welt mit hoher Präzision im Kleinen. Können die beiden unterschiedlichen Theorien zur Quantengravitation vereinheitlicht werden ?

Autor:
Die Allgemeine Relativitätstheorie (ART) ist eine stetige Theorie. Für Raum und Zeit gilt der Grenzwert → 0. Dadurch entstehen Singularitäten. Eine Singularität ist das schwarze Loch. Auch der Urknall ist eine Singularität. Singularitäten werden durch die ART nicht beschrieben. Den ersten Versuch, die ART zu quantisieren und die Unendlichkeiten zu vermeiden, haben Kaluza und Klein unternommen. Kaluza hat vor 100 Jahren die Allgemeine Relativitätstheorie von Einstein in 5 Dimensionen formuliert und auch zur Überraschung von Einstein festgestellt, dass die 5-dimensionale ART die Maxwell-Gleichungen enthält. Klein hat den Elektromagnetismus, der von den Maxwell-Gleichungen beschrieben wird, einem Kreis mit dem Durchmesser der Plancklänge zugewiesen und prägte den Begriff der 5. Dimension. Er hat erkannt, dass es den mathematischen Punkt in der Physik nicht gibt. Das Problem ist, dass die Plancklänge mit 10^-35 m und die Planckzeit mit 10^-43 s Experimenten nicht zugänglich sind. Da zu dieser Zeit die aufkommende Quantenmechanik interessantere Perspektiven versprach, wurde die Kaluza-Klein nicht weiter verfolgt.

IZ: Die Planckgrößen von Raum und Zeit , die Max Planck vor über 100 Jahren eingeführt hat, haben für die Quantengravitation bisher keine zufriedenstellenden Ergebnisse gebracht. Sie stellen eine Denkblockade dar. Auch die Superstring-Theorie, die als Quantengravitation gehandelt wird, initiiert keine Experimente, um theoretische Aussagen zu überprüfen. Was wäre die Alternative ?

Autor:
Eine Alternative wäre statt der Plancklänge 10^-35 der Durchmesser des kleinsten Teilchens , das durch Gravitation wechselwirkt. Das kleinste Teilchen ist das stabile Wasserstoffatom mit dem Durchmesser 10^-13 . Wasserstoffatome wechselwirken durch Gravitation und ballen sich zu Wasserstoffwolken zusammen. Kaluza und Klein kannten zu ihrer Zeit die Gravitation in Form der ART und den Elektromagnetismus in Form der Maxwell- Gleichungen. Die schwache und die starke Kernkraft waren damals noch nicht hinreichend erforscht. Die schwachen und die Farbladungen sind inzwischen experimentell ermittelt. Ihre Ladungen sind im Wasserstoffatom erhalten, und sie treten daher außerhalb des Wasserstoffatoms nicht in Erscheinung. Die elektrische Ladung vermittelt die Kraft zwischen dem Elektron und dem Atomkern. Die elektromagnetische Kraft hat wie die Gravitationskraft eine unendliche Reichweite, andernfalls können wir die Wasserstoffwolken in den Galaxien, wie in unserer Milchstraße, nicht durch die elektromagnetische und nicht sichtbare Radiostrahlung wahrnehmen. Die Massen der Elementarteilchen sind positiv . Es gibt keine negativen Massen. Daher gibt es für Massen auch keinen Erhaltungssatz.

IZ:
Das Wasserstoffatom ist die Schnittstelle zwischen der ART und der Quantenmechanik. Die ART gilt für > 10^-13m , die Quantenmechanik gilt bis < 10^-13m. Innerhalb des Wasserstoffatoms mit < 10^-13 m tragen die Quarks und das Elektron zwar Massen, aber die anderen 3 Kräfte überwiegen die Gravitationskraft. Bekannt ist das Verhältnis von der elektromagnetischen und der Gravitationskraft zwischen dem Elektron und dem Proton , das mit 10^36 angegeben wird. Die Gravitationskraft ist innerhalb des Wasserstoffatoms nicht messbar, wenn wir die schweren Massen von Elektron und Proton in Beziehung setzen. Es macht mehr Sinn, innerhalb des Wasserstoffatoms von trägen Massen auszugehen. 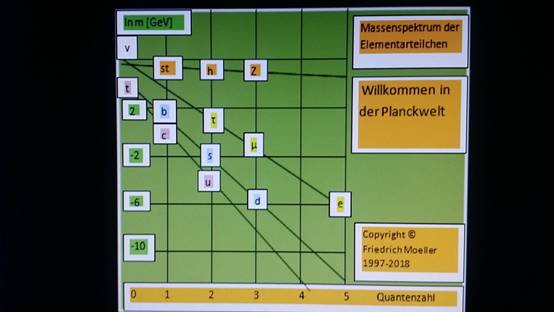Wenn wir von Quantengravitation sprechen und mit der Quantisierung von Raum und Zeit nicht weiter kommen, kann das Massenspektrum der Elementarteilchen nicht eine Quantenstruktur aufweisen ? Quantenstruktur heißt, die Massen lassen sich durch Quantenzahlen darstellen. Bekanntlich sind die Massen des Standardprogramms eines der großen Rätsel der Physik. Ein zu Grunde liegendes Muster der Massen ist nicht bekannt.

Autor:
Es ist schon erstaunlich. Wir regen Wasserstoffatome mit Licht an und entdecken, dass das Wasserstoffatom mit seinem Elektron nur bestimmte Frequenzen absorbiert. Diese Frequenzen lassen sich berechnen und in Quantenzahlen ausdrücken. Denken wir an die Balmer-Formel. Wir haben kein Kontinuum sondern ein Quantenspektrum. Dann regen wir das Wasserstoffatom mit größeren Energien an, indem wir Wasserstoffkerne in Beschleunigern aufeinander schießen. Wieder erhalten wir kein Kontinuum der Massen, sondern diskrete Massenwerte. Es gelingt uns, die Elementarteilchen durch Anwendung von Symmetrien im Massenspektrum der Elementarteilchen hinsichtlich des Spins und der elektrischen Ladung zu schematisieren. Aber es gelingt der herrschenden Lehre nicht, in diesem Schema für die Massen Quantenzahlen nachzuweisen.

IZ:
Wir können also die Gravitation im Wasserstoffatom nicht messen, wenn wir von der schweren Masse ausgehen, obwohl die Quarks als Bestandteile des Atomkerns und das Elektron eine Masse und damit Gravitationsladungen tragen. Das gilt auch für die Gesamtheit der Elementarteilchen, die durch die Kollision der Wasserstoffkerne in den Beschleunigern entstehen. Warum finden wir in den Massen der Elementarteilchen keine Ordnung ?

Autor:
Das Standardmodell der Elementarteilchen ist eine großartige Leistung der Wissenschaft. Ein Triumph war die Vereinheitlichung der elektromagnetischen und der schwachen Kraft zur elektroschwachen Kraft und der Nachweis der zugehörigen 4 Kraftteilchen. Das zugrunde liegende Prinzip ist die Eichsymmetrie. Mit der Eichsymmetrie konnte auch die starke Kernkraft, sie wird auch Farbkraft genannt, erfolgreich beschrieben werden. Die Gravitationskraft gehorcht dieser Eichsymmetrie nicht und daher können die Massen auch nicht durch das Eichprinzip berechnet werden. Im Standardmodell der Elementarteilchen ist neben der Eichsymmetrie noch eine weitere Symmetrie verborgen, und das ist die Skalensymmetrie. Tragen wir die Massenwerte logarithmisch auf, dann erhalten wir bei den 3 Generationen gleiche Abstände. Die Abstände sind abhängig von der elektrischen Ladung und vom Spin. Die 3 Generationen, auch Familien genannt, sind selbstähnlich. Sie unterscheiden sich nur durch die Massen. Wären im Standardmodell der Elementarteilchen die Massen alle 0, dann würden sich die 3 Familien nicht unterscheiden, und es gäbe nur eine Familie, und die Eichsymmetrie bliebe erhalten. Das große Problem wurde durch den Higgsmechanismus gelöst. Durch die spontane Symmetriebrechung bleibt die Eichsymmetrie erhalten, und die Elementarteilchen behalten die Massen, die sie durch die Stoßexperimente erhalten.



IZ:
Fassen wir nochmals zusammen: Die elektromagnetische Kraft , die schwache Kraft und die starke Kraft im Wasserstoffatom basieren auf der Eichsymmetrie. Die Massen werden durch den Higgsmechanismus eingeführt, damit das Standardmodell der Elementarteilchen mit den experimentell ermittelten Massen funktioniert. Kommen wir zurück auf die anfangs gestellte Frage. Ist die Gravitationskraft quantisiert ? Sind die 15 Massen des Standardmodells Gravitationsladungen ?

Autor:
Die Gravitationskraft des einzelnen Wasserstoffatoms ist nicht messbar. Betrachten wir die riesigen Wasserstoffwolken in den Galaxien und am Rande der Galaxien, dann ist die Gravitationskraft wohl messbar und nachweisbar. Gehen wir über zur Skalensymmetrie, dann kommen wir zum Wasserstoff, der aus den Quarks und dem Lepton der 2. Familie besteht. Dieser ultraschwere Wasserstoff {ccs µ} ist 4 bis 6 mal so schwer wie der Wasserstoff {uud e} , den wir kennen, und er hat damit die Gravitationskraft, die wir der Dunklen Materie zuschreiben. Wir können die Dunkle Materie durch die Skalensymmetrie erklären. Mit den aktuellen Forschungsergebnissen am LHC und dem Nachweis der Xi ccu ++ Teilchen kommen wir dem Rätsel der Dunklen Materie näher. Zu dieser Teilchenfamilie gehört auch das Xi ccd +. Das ist das ultraschwere Proton, das sich vom normalen Proton nur durch die Masse unterscheidet. Das ultraschwere Proton muss nochmals nachgewiesen werden. Erste Ergebnisse gab es vor 15 Jahren in den USA. Sie konnten nicht reproduziert werden. Xi ccd + Teilchen sind kurzlebig und zerfallen über Zwischenstufen zum normalen Proton . Dunkle Materie zerfällt zur sichtbaren Materie. Aus ultraschweren Wasserstoff entsteht normaler Wasserstoff. Die Gravitation unterscheidet zwischen Dunkler und sichtbarer Materie.

IZ:
Das ist ein interessanter Ansatz, die Dunkle Materie mit bekannten Teilchen des Standardmodells der Elementarteilchen zu erklären. WIMPS, Axionen und supersymmetrische Teilchen wären nicht notwendig. Die Teilchen der Dunklen Materie können am LHC hergestellt und untersucht werden. Was ist eigentlich der Ursprung der Dunklen Materie ?

Autor:
Der Ursprung der Dunklen Materie ist die Dunkle Energie. Die Dunkle Energie ist thermische Energie, die in den Fluktuationen des Vakuums steckt. Fluktuationen sind Temperatursprünge. Beim Urknall gab es noch keine Materie und kein Raum und keine Zeit, sondern nur thermische Energie. Aus dieser Energie ist dann durch Abkühlung die Dunkle Materie durch Symmetriebrechung entstanden. Jetzt schätzen wir die Dunkle Energie auf einen Anteil von 70 %, die Dunkle Materie auf 25 % und die sichtbare Materie auf 5 %.

IZ:
Wir suchen eine übergreifende Theorie zur Allgemeinen Relativitätstheorie und der Quantentheorie. Es besteht weitgehend Einigkeit darüber, dass die übergreifende Theorie, die oft als Weltformel bezeichnet wird, keine stetige Theorie wie die ART, sondern eine Quantentheorie sein soll. Welche Größe soll quantisiert werden ? Die Plancklänge und die Planckzeit, wie zur Zeit in den Superstringtheorien diskutiert, können die Größen nicht sein, weil sie keinen Zugang zu Experimenten liefern können. Sie haben eine Theorie der Quantengravitation entwickelt. Was zeichnet diese Theorie gegenüber der Superstringtheorie aus, die derzeit als der Favorit unter den Quantengravitationstheorien gehandelt wird ?

Autor:
Basis der Superstringtheorie ist die Lichtgeschwindigkeit c , das Wirkungsquantum h und Strings mit der Planklänge, die in 10 Raum-Dimensionen schwingen. Werden die 10 Raumdimensionen auf die 4-dimensionale Raumzeit herunter gebrochen, gibt es 10^500 Lösungen. Das ist absurd. Eine neue Variante ist die M-Theorie in 11 Dimensionen. Die Quantengravitation, die ich verfolge, geht aus von den empirisch ermittelten Massenwerten der massiven Elementarteilchen des Standardmodells. Diese Massenwerte werden vom Vakuumerwartungswert v , von der Eulerschen Zahl e und den Quantenzahlen von 0 bis 5 abgeleitet. Die Zahl der freien Parameter wird dadurch reduziert. Der geometrische Hintergrund von Raum und Zeit taucht in den Gleichungen nicht auf.

IZ:
Die Superstringtheorie erhebt den Anspruch, dass sie auch die Singularitäten der ART , hierzu gehören die Schwarzen Löcher, erklären kann. Stephen Hawking war überzeugt, dass neben der Allgemeinen Relativitätstheorie und der Quantentheorie die Thermodynamik als weitere dritte Theorie in das Welterklärungsmodell mit einbezogen werden muss. Für Stephen Hawking spielt die Entropie eine wichtige Rolle in der Theorie der Schwarzen Löcher. Das Schwarze Loch ist von einem Ereignishorizont umgeben, dessen Fläche in Entropie-Einheiten gemessen wird. Die Entropie gehört neben der Temperatur zu den fundamentalen Größen der Thermodynamik. Wenn wir die Entropie aus didaktischen Gründen auch als Wärmeladung verstehen, dann ist impliziert, dass die Entropie quantisiert ist. Eine wichtige Formel der Thermodynamik ist die Formel S/k = lnW . Gehen wir davon aus, dass die Bolzmannkonstante k das Entropiequantum ist, dann ist der Logarithmus der Wahrscheinlichkeit kein Kontinuum. Stephan Hawking erklärte die Singularität des Schwarzen Lochs mit Hilfe der Entropie. Können wir auch das Massenspektrum des Standardmodells mit der Entropie erklären ?

Autor:
Der Higgsmechanismus führt die Massen in das Standardmodell ein, ohne dass die Eichsymmetrie verletzt wird. Er hat sich gegenüber anderen Theorien durchgesetzt, weil er die wenigsten Widersprüche aufweist. Die Massenwerte selbst kann er auch nicht erklären. Das Prinzip des Higgsmechanismus besteht darin, dass die Massen auf den Vakuumerwartungswert v reduziert werden. Dieser reduzierte Massenwert f= m/v ist dimensionslos und wird Yukawa- Kopplungskonstante genannt. Die Symmetrie wird spontan gebrochen.

IZ:
Die spontane Symmetriebrechung ist auch beim Beispiel des magnetisierbaren Eisens zu beobachten. Über der Curietemperatur ist der Spin der Eisenatome regellos über den Kristall verteilt und das Eisen ist unmagnetisch. Die Symmetrie ist erhalten. Bei der Abkühlung unter den Curiepunkt wird die Symmetrie spontan gebrochen und es kommt zur Ausbildung von den Weißschen Bezirken, in denen sich der Spin parallel ausrichtet, die dann eine magnetische Wirkung aufweisen. Können Sie anhand eines anderen Beispiels den Ursprung der Masse durch Wärmeladungen aufzeigen ?

Autor:
Stellen Sie sich ein Glas gefüllt mit Wasser vor, das auf über 100 °C aufgeheizt wird. Es entsteht Wasserdampf. Wasserdampf ist gasförmiges Wasser, bei dem die Wassermoleküle sich regellos durcheinander bewegen, sich gegenseitig anstoßen und auch gegen die Glaswand stoßen. Wasserdampf ist scheinbar schwerelos. Kühlt der Wasserdampf unter 100 °C ab, kondensiert der Wasserdampf. Es entstehen Wassertropfen. Sie erhalten Masse und bewegen sich aufgrund der Schwerkraft entlang der Glaswand nach unten. Bei der Kondensationstemperatur von 100 °C bleibt die Temperatur konstant, weil Kondensationswärme erzeugt wird, bis der gesamte Wasserdampf in Wasser umgewandelt wird. Diese Kondensationswärme wird auch Entropie genannt. Die Entropie entsteht nicht kontinuierlich sondern in Form von Wärmeladungen. Die Wassertropfen sind nicht beliebig groß, sondern ihre Größen sind in diesem Bild skalensymmetrisch und selbstähnlich. Dieses Bild können wir auf den Ursprung der Massen der Elementarteilchen übertragen. Massen sind kein Kontinuum , sondern sie haben definierte Werte, weil die Entropie wie das Wirkungsquantum quantisiert ist.

IZ:
Zum Schluss wollen wir noch eine der spannendsten Fragen der modernen Physik beantworten. Was ist eigentlich das Higgs-Boson ? Warum hat es gerade den Wert , den es hat ? Lässt sich der Wert berechnen ? Was ist das Higgsfeld ?

Autor:
Die Masse der Elementarteilchen ist keine ursprüngliche Eigenschaft des Teilchens wie die elektrische Ladung, sondern sie entsteht durch die Kopplung an das skalare Higgsfeld. Der auf den Vakuumerwartungswert v = 246 GeV reduzierte Wert m/v ist der Yukawa-Kopplungskoeffizient. Sein Wert ist für das Higgs-Boson e^-2/3. Der Wert , der 2011 für das Higgsboson am Atlasdetektor gemessen wurde, ist 126.3 GeV . In der QED von Feynman entspricht die Feinstrukturkonstante 1/137 der quantenmechanischen Wahrscheinlichkeit, mit der das Photon an die elektrische Ladung des Elektrons koppelt. Wenn wir analog die Kopplung an das Higgsfeld als thermodynamische Wahrscheinlichkeit definieren, können wir die Boltzmanngleichung S= k lnw umformulieren in W=e^(S/k). Für das Higgsboson erhalten wir dann mit W= e^-2/3 die Entropie bzw. Wärmeladung S=-2/3 k. Das Higgsfeld ist das skalare Temperaturfeld, dem Wärmeladungen entzogen werden. So trägt das Z-Boson die Wärmeladung -k , das top-Quark die Wärmeladung -1/3 k . Die Masse kann so auf der Grundlage der Thermodynamik erklärt werden. Wir haben auch eine Antwort auf das Hierarchieproblem des Higgsbosons. Seine Masse wird durch die Skalensymmetrie stabilisiert. Kommen wir zu einen weiteren wichtigen Aspekt zur Entropie. Zwischen Entropie und Information gibt es eine einfache Beziehung. 1 bit Information entspricht einer Wärmeladung von k ln2. In seiner Theorie der Schwarzen Löcher beschäftigte sich Stephen Hawking auch mit dieser Beziehung. Das Schwarze Loch ist von einem Ereignishorizont umgeben, dessen Fläche in Entropieeinheiten bzw. Wärmeladungen gemessen wird. Wenn das Schwarze Loch Materie verschluckt dann verschluckt es auch Information, die hinter dem Ereignishorizont unwiederbringlich verschwindet . Ist diese Information verloren ? Diese Frage beschäftigte Stephen Hawking .

IZ:
Gibt es die Weltformel ? , die die elektromagnetische Kraft, die schwache Kraft , die starke Kernkraft und die Gravitation zu einer Urkraft vereint ?

Copyright © Friedrich Moeller 1997-2020 email f.moeller@necnet.de