Willkommen in der Planckwelt

Gibt es die Weltformel ?

6. Interview in Hannover

IZ:
Peter Higgs feierte seinen 90. Geburtstag, und eines seiner großen Probleme ist nachwievor aktuell. Die Allgemeine Relativitätstheorie von Einstein und die Quantentheorie von Feynman u.a. wurden durch Beobachtung und Experimente mit hoher Präzision bestätigt. Wenn wir Gravitation und Quantentheorie zu einer gemeinsamen Theorie, die allgemein Weltformel genannt wird, vereinigen wollen, muss die Quantennatur der Gravitation empirisch nachgewiesen werden.

Autor:
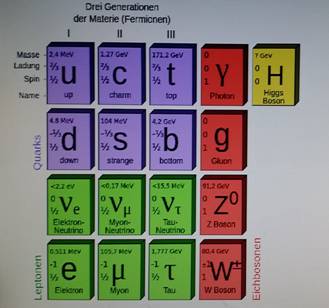
Massen sind Gravitationsladungen. Das Standardmodell ordnet die Elementarteilchen nach Spin und elektrischer Ladung. Die Massen der Elementarteilchen sind jedoch beliebig ohne jegliche Struktur und Ordnung. Sie können nicht berechnet und nicht von einer Naturkonstanten abgeleitet werden. Dieses Problem ist zu lösen, wenn wir die Quantennatur der Massen nachweisen wollen.

IZ:
Naturkonstanten haben revolutionäre Entwicklungen in der Physik ausgelöst. So begründet die Lichtgeschwindigkeit c die Spezielle Relativitätstheorie. Das Wirkungsquantum h begründet die Quantentheorie. Welche Naturkonstante begründet das Massenspektrum der Elementarteilchen?

Autor:
Diese Naturkonstante darf keine Dimension haben, wie c oder h. Sie muss skalierbar sein. Interessant sind hierbei transzendente Zahlen. Transzendente Zahlen sind Dezimalzahlen mit chaotischer Ziffernfolge. Von keinem Computer in der Welt können sie in Primzahlen zerlegt werden. Neben der transzendenten Zahl π und der Euler`schen Zahl e gibt es den Goldenen Schnitt ф = 1.681… mit dem Kehrwert Ф= 0.681 …. . Die Formel e^iπ = -1 ist als Formel auf T-Shirts schon lange bekannt. Mit der Erweiterung e^iπ+ф=Ф wird der Goldene Schnitt in die Formel einbezogen.

IZ:
Unseren materiellen Wohlstand haben wir der Wissenschaft und der Technik zu verdanken. Durch Experimente werden Gesetze aufgedeckt und in mathematische Formeln gefasst. Die mathematischen Formeln komprimieren das Wissen und werden von Generation zu Generation weitergegeben. Unser technisches Umfeld basiert auf der Mathematik. Können wir mit transzendentalen Zahlen die 4 Grundkräfte vereinigen?

Autor:
Die 4 Grundkräfte sind die elektromagnetische, die schwache, die starke und die Gravitationskraft. Kraftvermittelnde Teilchen koppeln an die jeweiligen Felder mit ihren Kopplungskonstanten an. Beginnen wir zunächst mit der Kopplungskonstante der elektromagnetischen Wechselwirkung, die von Sommerfeld vor über 100 Jahren als Feinstrukturkonstante α eingeführt wurde. Ihr Wert 1/137 ist nachwievor ein Rätsel. Warum hat sie den Wert 137 und nicht 138 oder 139 oder 141?

IZ:
Warum ist die Zahl 137 als Kehrwert der Feinstrukturkonstanten bis in unsere Zeit so mysteriös? Die elektromagnetische Wechselwirkung wird durch die Quantenelektrodynamik (QED) beschrieben, die in den 40-iger Jahren u.a. von Feynman entwickelt wurde. In seinen Feynman- Diagrammen spielt die Zahl 1/137 eine zentrale Rolle. Das Photon koppelt als Eichboson an die elektrische Ladung des Elektrons und des Positrons mit der Wahrscheinlichkeit 1/137. Kann die Zahl 1/137 von einer transzendenten Zahl der Formel e^iπ +ф=Ф abgeleitet werden ?

Autor:
Die dimensionslose Zahl 137 hat die berühmten Physiker Richard Feynman und Wolfgang Pauli bis an ihr Lebensende beschäftigt. Physiker haben diese Zahl am Anfang ihrer Karriere an die Laborwand geheftet. Sie wollten den Zettel erst entfernen, wenn sie das Rätsel dieser Zahl gelöst haben sollten. Die Feinstrukturkonstante 1/137= e²/h c verknüpft die elektrische Ladung e des Elektromagnetismus mit der Lichtgeschwindigkeit c der speziellen Relativitätstheorie und mit dem Wirkungsquantum h der Quantenmechanik. Die mysteriöse Zahl 137 finden wir auch beim Goldenen Winkel 137 °, der vom Goldenen Schnitt abgeleitet wird. So ist arc 137 = 2π -2π /Ф. arc α ist die Bogenlänge des Kreises. Ein anschauliches Beispiel der Evolution ist die Sonnenblume. Ihre Blätter und Blüten sind um den Goldenen Winkel 137° versetzt und sie erhalten damit wegen der fehlenden Periodizität die maximale Sonneneinstrahlung.

IZ:
Die Kopplungskonstante des Photons 1/137 wird von den transzendenten Zahlen π und Ф abgeleitet. Wir leiten jetzt die Kopplungskonstante des Z-Bosons , dem Eichboson der schwachen Wechselwirkung, von der transzendenten Zahl e aus der Formel e^iπ +ф=Ф ab. Das Z-Boson wird auch als das schwere Photon bezeichnet.

Autor:
Nach dem Higgsmechanismus wird die Masse der Elementarteilchen berechnet nach der Formel m= v f . Die Proportionalitätszahl v= 246 GeV ist der Vakuumerwartungswert der elektroschwachen Wechselwirkung und f ist der Yukawa-Kopplungskoeffizient. Überraschenderweise ist der Kopplungskoeffizient des Z-Bosons e^-1 . Die berechnete Masse für das Z-Boson ist 90,5 GeV. Der experimentelle Wert nach Wikipedia ist 91.2 GeV . Die Abweichung vom berechneten Wert ist <1 % .

IZ:
Das Z-Boson und die beiden W^+--Bosonen sind die Eichbosonen der schwachen Kraft. Mit welchem Problem wurden wir beim Z-Boson konfrontiert ?

Autor:
Da das Z-Boson wegen der kurzen Reichweite der schwachen Kraft eine Masse haben muss, gab es ein Problem mit der Eichsymmetrie und ihrer Phaseninvarianz. Die Bedeutung der Eichsymmetrie wurde erstmals in den Gleichungen von Maxwell erkannt. Sie hat sich bewährt bei der Entwicklung der Quantenelektrodynamik (QED) und wurde als tragfähiges Symmetrieprinzip auf die schwache Wechselwirkung angewandt. Die Eichsymmetrie bleibt in den Bewegungsgleichungen nur erhalten, wenn die Teilchen keine Masse haben. Massen zerstören die Eichsymmetrie, und das war 40 Jahre lang ein Problem. Schließlich hat sich der Higgsmechanismus durchgesetzt, der den 3 Eichbosonen Masse verschafft, das Photon masselos lässt und dabei die Eichsymmetrie durch spontane Symmetriebrechung aufrechterhält. Das Z-Boson wurde 1983 am CERN nachgewiesen.

IZ:
Die Eichsymmetrie hat sich als Symmetrieprinzip in der Quantentheorie durchgesetzt. Was macht das Wesen der Eichsymmetrie aus?

Autor:
Physiker unterscheiden zwischen der globalen und der lokalen Eichsymmetrie. Bei der globalen Eichsymmetrie ändert sich die Wellenfunktion ψ(x,t) nicht, wenn sie mit der Phase e^iθ multipliziert wird. Feynman hat iθ durch das Wirkungsintegral iA/h ersetzt. A ist die Wirkung. Damit wird die globale Eichsymmetrie zur lokalen Eichsymmetrie, die jetzt von Ort und Zeit abhängig ist. Wieder begegnet uns die Euler`sche Zahl aus der Gleichung e^iπ+ф=Ф . Die lokale Eichsymmetrie erzeugt einen zusätzlichen mathematischen Term, der für die elektromagnetische Kraft steht. Das macht die lokale Eichsymmetrie auch für die Entwicklung der elektroschwachen Kraft interessant, die die schwache Kraft mit der elektromagnetischen Kraft vereinigt.

IZ:
Higgs hat das nach ihm benannte Higgsboson postuliert, das als Anregung des Higgsfeldes für Experimente zugänglich ist.
Die größte Herausforderung ist nachwievor, die Masse des Higgsbosons zu berechnen. Die Masse ist der einzige Parameter, der mit dem Higgsmechanismus nicht berechnet werden kann. Wäre die Masse des Higgs-Bosons bekannt gewesen, hätte man sich den experimentellen Aufwand am LHC sparen können und die Detektoren gezielt auf den berechneten Wert ausrichten können. Kann die Masse des Higgs-Bosons von der transzendenten Euler`schen Zahl e abgeleitet werden ?

Autor:
Der Higgsmechanismus lässt viele Fragen offen . Warum hat das Higgs-Boson gerade die Masse hat, die gemessen wurde? Wie kommt das Higgs-Boson zu seiner Masse ? Wie kann das Higgs-Boson dem top-Quark eine Masse verleihen, die viel größer ist als die Masse des Higgs-Bosons ? Auf diese Fragen gibt die Quantengravitation eine Antwort, und sie lässt sich auch mit dem Higgsmechanismus vereinbaren. Die Masse des Higgsbosons berechnet sich zu m_H=v e^-2/3 = 126.3 GeV . Das ist genau der Wert, der 2012 am ATLAS-Detektor gemessen wurde. Inzwischen ist der offiziell experimentell ermittelte Wert nach Wikipedia 125.3 GeV . Mit aufwändigen Versuchsreihen tasteten sich die Physiker an diesen Wert heran. Im Standardmodell werden neben der lokalen Eichsymmetrie zwei weitere Symmetrien benötigt. Mit der Skalensymmetrie und der SO(4) – Symmetrie können wir die Massen des Standardmodells durch die Kopplung an das Higgs-Boson berechnen, z.B. m_Z = m_H e^-1/3 .

IZ:
Mit der Masse des Higgs-Bosons ist eines der großen Rätsel der Physik verbunden, die fehlende Natürlichkeit. Eigentlich sollte das Higgs-Boson gar nicht die Masse haben, die es hat. Das Rätsel wird seit 2012 heiß diskutiert.

Autor:h
Das Higgs-Boson hat als Skalarboson den Spin 0 und ist elektrisch neutral. Es wechselwirkt mit den Quantenfluktuationen. Die Energie insbesondere durch die Gravitations-Quantenfluktuationen schaukelt die Higgs-Masse hoch bis zu einer Zahl mit 18 Nullen. Das macht die Theorie unnatürlich. Welcher Effekt zwingt die Masse des Higgs-Bosons in die Fermi-Skala der elektroschwachen Wechselwirkung ? Diskutiert wird die Feinabstimmung mit supersymmetrischen Teilchen, die bisher am LHC noch nicht nachgewiesen wurden. Vergleichbar ist der Effekt mit der UV-Katastrophe beim Spektrum des Schwarzen Strahlers am Anfang des 20. Jahrhunderts. Nach der damals herrschenden Theorie ging die Strahlungsenergie mit steigender Frequenz gegen unendlich. Max Planck löste das Problem mit der Einführung des Wirkungsquantums h und begründete damit die Quantentheorie. Wird das Higgs-Problem durch die Quantengravitation und das Entropiequantum k gelöst?

Autor:
Es gibt zwei Anwärter für die Quantengravitation. Die Schleifen-Quantentheorie geht davon aus, dass Raum und Zeit körnig sind. Der kleinste Abstand ist die Plancklänge und die Planckzeit. In der Superstringtheorie gibt es keine Punktteilchen, die zu mathematischen Unendlichkeiten führen, sondern Strings mit der Plancklänge 10^-35 m. Jedes Elementarteilchen hat sein eigenes Schwingungsspektrum. Erst wenn Strings in 10 Dimensionen schwingen, werden mathematische Unendlichkeiten vermieden. Die Superstringtheorie mit ihren 10 nicht vorstellbaren Raumdimensionen sind mathematische Theorien, die keine experimentellen Ergebnisse bestätigen oder voraussagen können. Sie erklären auch nicht das Massenspektrum der Elementarteilchen.

IZ:
Beide Theorien der Quantengravitation arbeiten an der Planckskala. Strings mit der Plancklänge 10^-35 sind Experimenten nicht zugänglich. Die notwendige Energie und der notwendige Impuls sind nach der Unschärferelation von Heisenberg mit Beschleunigern überhaupt nicht zu erreichen. Beschleuniger müssten größer als die Milchstraße sein. Wir gehen daher einen anderen Weg. Wir können die Quantennatur der Gravitation nachweisen, wenn wir die kleinsten gemessenen Massen als Quanten darstellen.

Autor:
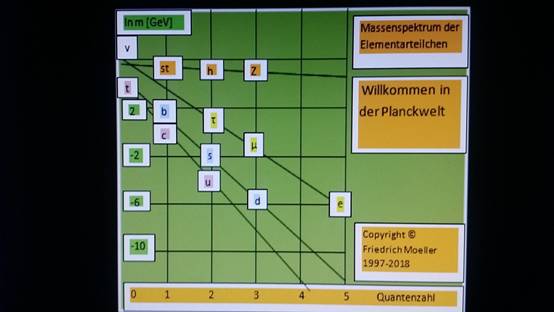
Die kleinsten Massen, die gemessen wurden, sind die Massen der Elementarteilchen im Standardmodell. Ihre Werte können nach herkömmlicher Meinung nicht erklärt und berechnet werden. Im rechten Masse-Diagramm haben die Massen, logarithmisch aufgetragen, die Quantenzahlen 0,1,2,3,5. Die Massen der Quarks und geladenen Leptonen der 3 Familien der Quarks und Leptonen sind skalensymmetrisch. Sie haben auf den 4 unterschiedlich geneigten Geraden gleiche Abstände. Die Gravitation wird im Standardmodell vernachlässigt, weil das Verhältnis der elektromagnetischen Kraft zur Gravitationskraft beim Proton und beim Elektron 10^36 ist. Beim Wasserstoffatom ist die Gravitation beobachtbar, weil sich die elektrischen, die schwachen und die Farbladungen durch die Ladungserhaltung aufheben. Im Makrokosmos ziehen sich die Wasserstoffatome durch die Gravitation in Wasserstoffwolken zusammen, sie verdichten sich, und es entstehen die Sterne.

IZ:
In der rechten Grafik tragen die Massen Quantenzahlen. Die Neigungswinkel der 4 Geraden sind nicht beliebig, weil die SO(4) Symmetrie die Massenwerte festlegt.

Autor:
Wenn dem so ist, können wir die Symmetrien zusammenfassen zu SO(4) x SU(3) x SU(2) x U(1) . Ihre Annahme hat einen gewissen Charme. So wie das Photon mit der elektrodynamischen Wahrscheinlichkeit α =1/137 an das elektromagnetische Feld ankoppelt, so koppeln die 15 Elementarteilchen des Standardmodells mit ihren Yukawa-Kopplungskonstanten an das Higgsfeld . Die Yukawa-Koeffizienten sind die thermodynamischen Wahrscheinlichkeiten nach der umformulierten Bolzmanngleichung W=e^-S/k. Die Massen der Elementarteilchen im Standardmodell sind im Bereich der Fermi-Skala der elektroschwachen Wechselwirkung und werden von der transzendenten Euler´schen Zahl e abgeleitet und wie folgt berechnet:

Für die massiven Eichbosonen gilt :
H Z m = v e^ ( -e°/3 n ) n = 2,3

Für die geladenen Leptonen gilt :
τ μ e m = v e^(+ e^-2/3 –e n ) n=2,3,5

Für das hypothetische X17 – Teilchen gilt:
X17 m=2 v e^( + e^-2/3 - e n ) n= 4

Für die Quarks gilt:
b s d m = v e^ ( -1/3 - e²/2 n ) n = 1,2,3
t c u m = v e^ ( -1/3 -2 e²/3 n ) n = 0,1,2

Für die Neutrinos gilt:
v_τ ν_μ ν_e m = v e^ (+ e^-2/3 –e² n ) n=1,2,4

Die Familienzahlen sind Quantenzahlen . Die Steigungen der Geraden sind eine Funktion der Eulerschen Zahl e . Die Geraden sind längs der ln m –Achse verschoben. Wir können das auch so interpretieren, dass Bosonen, Quarks und Leptonen unterschiedliche Vakuumerwartungswerte haben.

Neu ! Das X17 und das Dunkle Elektron

IZ:
Wenn wir dem Massenspektrum des Standardmodells eine SO(4) – Symmetrie mit 4 Gravitationsladungen zuschreiben, dann müssen wir auch erklären, was diese Gravitationsladungen sind.

Autor:
Die Entropie S in der umformulierten Bolzmanngleichung W=e^-S/k ist wie die Temperatur eine wichtige Größe der Thermodynamik und spielt in der Theorie der Schwarzen Löcher eine wichtige Rolle. Das Schwarze Loch besteht aus reiner Gravitation und wird definiert durch die Masse, die elektrische Ladung, den Drehimpuls und den Ereignishorizont. Nach Wheeler besteht die Fläche des Ereignishorizontes aus winzigen Quadraten mit der Plancklänge². Nachdem Wheeler den Quadraten keine Bedeutung zumessen konnte, hat Hawking die Fläche des Ereignishorizonts mit der Entropie gleichgesetzt. Am Ereignishorizont bleibt die Zeit stehen und es entsteht die Hawking-Strahlung als eine reine Temperaturstrahlung. Aus didaktischen Gründen wird die Entropie neuerdings auch Wärmeladung genannt. Das ist auch ein Hinweis darauf, dass die Entropie aus Ladungen besteht und wie die Wirkung Quanteneigenschaften hat.

IZ:
Kommen wir beim Schwarzen Loch zu einem epochalen Ereignis . 2019 ist erstmals ein schwarzes Loch sichtbar gemacht worden anhand der Photonen des Infrarotspektrums.

Autor:
Mit dem ersten Bild (EHT / dpa) des Schwarzen Lochs in 55 Millionen Lichtjahren Entfernung in der Galaxie Messier 87 wurden die Wärmeladungen sichtbar gemacht. Die sich um das Schwarze Loch drehende Materie heizt sich durch Reibung extrem auf, bevor sie im Schlund des Schwarzen Lochs verschwindet. Mit der Entropie haben wir eine Größe, die wir vom Makrokosmos der Schwarzen Löcher bis zum Mikrokosmos des Standardmodells skalieren können. Die Entropie ist quantisiert. Die Bolzmannkonstanten k ist das Entropiequantum . Kommen wir jetzt zurück zu den 4 Ladungen der SO(4) Symmetrie.

IZ:
Fassen wir die Überlegungen nochmals zusammen. Im Standardprogramm koppeln 15 massive Elementarteilchen mit 4²-1 = 15 Yukawa- Kopplungskonstanten an den Vakuumerwartungswert v. So wie Feynman mit dem Eichfaktor e^i A/ h die lokale Eichsymmetrie erzeugte, können wir analog mit e^-S/k das Massenspektrum der Elementarteilchen erzeugen. Elementarteilchen werden definiert durch Masse, elektrische Ladung und Spin. Schwarze Löcher werden definiert durch Masse, elektrische Ladung und Drehimpuls.

Autor:
In der obigen Grafik tragen die Massen die Quantenzahlen 0,1,2,3,5 . Die Massen sind auf Geraden, die um definierte Winkel gedreht und längs der ln y-Achse verschoben sind. Das ist durch die SO(4)-Symmetrie, die aus einer 3D- Rotation und einer Translation besteht, gewährleistet. Auf der oberen Bosonen-Gerade sind das Higgsboson und das Z-Boson. Darunter ist die Leptonen-Geraden mit der elektrischen Ladung – 1. Darunter sind die beiden Quark-Geraden mit den elektrischen Ladungen -1/3 und +2/3. Neutrinos haben im Standardmodell keine Masse. Die SO(4) Symmetrie gibt den Drehwinkeln und den beiden Verschiebungen definierte Werte vor. Eine Symmetrie beendet die Beliebigkeit. Der tan der Drehwinkel ist -1/3 e° , - e , 2/3 e² , ½ e² . Die Drehwinkel stehen für die 4 unterschiedlichen Wärmeladungen der Bosonen, geladenen Leptonen und der beiden Quarks. Die Quanten der Gravitation werden auf die natürliche Zahl e und auf Quantenzahlen zurückgeführt. Die Kopplungskonstante der starken Wechselwirkung nehmen wir an mit e^0 =1 . Die Kopplungskonstanten der schwachen Wechselwirkung, der elektromagnetischen Wechselwirkung und der Gravitation werden von den transzendenten Zahlen aus der Gleichung e^iπ+ф=Ф abgeleitet.

IZ:
Wie werden die 4 Naturkräfte vereinigt?

Autor:
Das Standardprogramm der Elementarteilchen wird allgemein als unvollständig angesehen, weil es die Gravitation nicht enthält. Kräfte werden durch Symmetrien dargestellt. Wenn wir das Standardmodell durch die Symmetrien SO(4) x SU(3) x SU(2) x SU(1) erweitern, erhalten die Massen der Elementarteilchen eine Struktur und werden als Gravitations-Ladungen in das Standardprogramm einbezogen. Die Teilchen-Familien werden Quantenzahlen. Wir können uns die Vereinigung der 4 Grundkräfte durch fortgesetzte Symmetriebrechungen vorstellen, vom Ellipsoiden der Gravitationskraft zur Kugel der starken Kraft, zur Scheibe der schwachen Kraft und zum Kreis der elektromagnetischen Kraft. Die Formel e^iπ+ф=Ф zeigt die Bedeutung der Eulerschen Zahl e als Naturkonstante für die Vereinigung der Naturkräfte. Mit der Konstanten e, dem Vakuumerwartungswert v und den Quantenzahlen können die Massen der Elementarteilchen des Standardprogramms hergeleitet werden. Die natürliche Zahl e ist der Ursprung der Masse. Hätte die Eulersche Zahl den Wert 2, hätten wir eine andere Welt oder die Welt würde nicht existieren. Das gilt auch für die Masse des top-Quarks, das 1995 in den USA am Tevatron nachgewiesen wurde. Mühsam über Jahre arbeiteten sich die Physiker Schritt für Schritt von 20 GeV bis an die Masse von 173 GeV heran. Niemand verstand, warum die Masse des top-Quark so hoch sein sollte. In beiden Fällen gibt die Quantengravitation und die Skalensymmetrie eine Orientierung. Sie erklärt warum das top-quark , das Higgsboson und das Z-Boson genau die Werte haben, die am LHC gemessen werden mit der Higgsformel m=v e^-n/3 mit n=1,2, 3.

IZ:
Eine physikalische Theorie ist erfolgreich, wenn sie nicht erklärbare Daten von Experimenten erklären, und wenn sie Voraussagen machen kann. Zu den gegenwärtigen Rätseln gehören der schwere Wasserstoff der Dunklen Materie, das supersymmetrische stop-Quark, die fehlende Natürlichkeit, das top-Quark, die 10-dimensionale Superstringtheorie, das Informationsparadox.

Autor:
Die Formel e^iπ+ф=Ф zeigt die Bedeutung der Euler` schen Zahl e als Naturkonstante. Mit der Konstanten e, dem Vakuumerwartungswert v und den Quantenzahlen können die Massen der Elementarteilchen des Standardprogramms hergeleitet werden. Die natürliche Zahl e ist der Ursprung der Masse. Das gilt auch für die Masse des top-Quarks, das 1995 in den USA am Tevatron nachgewiesen wurde. Mühsam über Jahre arbeiteten sich die Physiker Schritt für Schritt von 20 GeV bis an die Masse von 173 GeV heran. Niemand verstand, warum die Masse des top-Quark so hoch sein sollte. In beiden Fällen gibt die Quantengravitation und die Skalensymmetrie eine Orientierung. Sie erklärt warum das top-Quark , das Higgsboson und das Z-Boson genau die Werte haben, die am LHC gemessen werden. Eine Erklärung hierfür gibt die Higgsformel m=v e^-n/3 mit n=1,2, 3.

IZ:
Die Existenz der Dunklen Materie ist unbestritten. Aus welchen Teilchen besteht die Dunkle Materie ? Kann sie mit den Elementarteilchen des Standardmodells erklärt werden, oder benötigen wir neue Teilchen jenseits des Standardmodells. Das ist derzeit eines der großen Rätsel der Physik. Viel Forschungsgeld steht hierzu zur Verfügung. Im Gespräch ist der Future Circular Collider (FCC) , der nächste Teilchenbeschleuniger mit einer Umfangslänge von 100 km. Mit ihm sollen neue Elementarteilchen, u.a. supersymmetrische Teilchen, jenseits des Vakuumerwartungswerts v zwischen der Fermi-Skala und der Planck-Skala detektiert werden.

Autor:
Die Sternenbewegung am Rand der Milchstraße inmitten der Wasserstoffwolken weichen vom Gravitationsgesetz Newtons ab. Die Geschwindigkeit der Wasserstoffwolken und der Sterne wird mit der Dopplerverschiebung der 21 cm – Linie des Wasserstoffs gemessen. Die Geschwindigkeit der Sterne ist so groß, dass sie eigentlich aufgrund der hohen Fliehkraft ins All geschleudert werden müssten. Die Wasserstoffatome müssten 4 bis 6 Mal so schwer sein, um die Gravitation zu erzeugen, die die Sterne auf ihrer beobachteten Bahn hält. Diese Gravitation wird der Dunklen Materie zugesprochen. Schwerer Wasserstoff, der aus den Quarks und dem Lepton der 2. Familie {ccs µ} besteht, ist 4 mal so schwer wie normaler Wasserstoff und würde die Gravitation erzeugen, die der Dunklen Materie zugeschrieben wird. Auf diese Weise kann die Skalensymmetrie der Quantengravitation die beobachteten Daten erklären. Am LHC wurde 2017 das erste Teilchen mit zwei schweren charm-Quarks nachgewiesen. Das Teilchen stammt aus der Xi-Familie {ccu++} . Wenn es am LHC gelingen sollte, das Xi-Teilchen {ccd+} zu erzeugen und nachzuweisen, erhielten wir das ultraschwere Proton und damit den schweren Wasserstoffkern. Wir bräuchten dann keine neuen exotischen Teilchen für die Dunkle Materie. Die Frage ist nicht, wie entsteht der Wasserstoff in den Wasserstoffwolken, sondern wie entsteht der ultraschwere Wasserstoff mit seiner 4 bis 6 fachen Gravitationswirkung, der in den normalen Wasserstoff zerfällt.

IZ:
Kommen wir zum nächsten Rätsel der Supersymmetrie. In der Grafik ist die Stelle der Bosonen-Geraden bei der Quantenzahl 1 nicht besetzt. Gibt es hierzu eine Erklärung?

Autor:
Das ist eine gute Frage ! Die Stelle mit der Quantenzahl 1 auf der Bosonen-Geraden entspricht der Masse 176 GeV . Die Masse 176 GeV erhalten wir auf zwei verschiedenen Wegen. Da ist einmal der Fermionen-Pfad mit t= v e^( -2e²/3 n - 1/3 ) mit der Quantenzahl n=0 und der Verschiebung -1/3 . Da ist zum anderen der Bosonen- Pfad mit t= v e^-n/3 mit der Quantenzahl 1 und der Verschiebung 0 . Das Teilchen auf der Bosonen-Geraden entspricht dem supersymmetrischen stop-Quark mit Spin 0, das allgemein als das leichteste supersymmetrische Teilchen angesehen wird. Es passt in das Massenspektrum des Standardmodells und wird durch die Quantengravitation vorausgesagt und berechnet.

IZ:
Wenn das top-Quark zusammen mit dem stop-Quark erzeugt werden sollte, wären da nicht die Erhaltungssätze der elektrischen Ladung und des Drehimpulses verletzt ? Sollte das stop-quark, wenn es existiert, nicht in den Zerfallsdaten des ATLAS-Detektors und des CMS-Detektors schon längst gefunden worden sein ?

Autor:
Das top-Quark ist ein außergewöhnliches Quark. Es hat eine Zerfallszeit von 10^-25 s und keine Zeit zum Hadronisieren. Als es 1995 am Tevatron nachgewiesen wurde, gab es Probleme, die elektrische Ladung +2/3 zu bestimmen. Es unterliegt allen 4 Wechselwirkungen. So wie bei der schwachen Wechselwirkung die Verletzung der Parität nachgewiesen wurde, so wurde bei der starken Kernkraft auch die CP-Verletzung nachgewiesen. Die bisherige CP-Verletzung reicht aber nicht aus, um das Fehlen der Antimaterie zu erklären. Das ist ein weiteres Rätsel, an dem mit großem Aufwand auf der ISS gearbeitet wird. Bis jetzt wurde auf der ISS nur ein geringer Positronen-Überschuss nachgewiesen.

IZ:
Die Superstringtheorie mit ihren 10 Raumdimensionen wird aktuell diskutiert. Dimensionen sind Freiheitsgrade. Müssen Dimensionen unbedingt die uns bekannten Raumdimensionen sein?

Autor:
Das Quark ist an allen 4 Wechselwirkungen beteiligt und gehorcht den Symmetrien SO(4) x SU(3) x SU(2) x U(1). Wir können uns das Quark als String mit 4+3+2+1 = 10 Ladungen vorstellen, der in 10 Dimensionen schwingt. Damit werden wir auch der vielen Varianten der Quarks mit unterschiedlichen Wärmeladungen, Farbladungen, Spin und elektrischen Ladungen gerecht. Jedes Quark hat dann sein eigenes Schwingungsspektrum in 10 Dimensionen.

IZ:
Beim Schwarzen Loch gibt es das ungeklärte Problem des Informationsparadoxons, das Stephen Hawking nicht mehr lösen konnte. Massen bestehen aus Ladungen. Die Ladungsstruktur entspricht der Information, die die Masse trägt. Was geschieht eigentlich mit der Information der in das Loch stürzenden Materie? Geht die Information durch die Hawking-Strahlung unwiederbringlich verloren?

Autor:
Die Information ist Negentropie und eine wichtige Größe der Thermodynamik. Für die Erzeugung von 1 Bit Information wird eine Entropie von kln2 benötigt. Das Entropiequantum entspricht einer Wärmeladung und Information entspricht einer negativen Wärmeladung. Wenn wir den Speicher eines Computers löschen, wird Wärme frei. Deshalb müssen auch Computer gekühlt werden. Wir haben Stephen Hawking u.a. zu verdanken, dass er der Thermodynamik und der Information einen eigenständigen Platz neben der Allgemeinen Relativitätstheorie und der Quantentheorie eingeräumt hat, um die Welt zu erklären. Bei der ART und bei der Quantentheorie ist die Zeit umkehrbar. Nach dem Informationsparadoxon sollte beim Zerstrahlen der Schwarzen Lochs die Information wieder zurückgewonnen werden. Wird die Thermodynamik auf das Schwarze Loch angewandt, verhindert die Entropie diesen umkehrbaren Prozess. Wenn bei einem Prozess Entropie erzeugt wird, ist die Zeit irreversibel.
Gibt es die Urkraft?

copyright © Friedrich Moeller 1997-2020 email: f.moeller@necnet.de